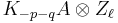Quillen–Lichtenbaum conjecture
In mathematics, the Quillen–Lichtenbaum conjecture is a conjecture relating étale cohomology to algebraic K-theory introduced by Quillen (1975, p. 175), who was inspired by earlier conjectures of Lichtenbaum (1973). Kahn (1997) and Rognes & Weibel (2000) proved the Quillen–Lichtenbaum conjecture at the prime 2 for some number fields. Rost and Voevodsky have announced proofs of the Bloch–Kato conjecture, which implies the Quillen–Lichtenbaum conjecture for all primes.
Statement
The conjecture in Quillen's original form states that if A is a finitely-generated algebra over the integers and l is prime, then there is a spectral sequence analogous to the Atiyah-Hirzebruch spectral sequence, starting at
![E_2^{pq}=H^p_\text{etale}(\text{Spec }A[\ell^{-1}], Z_\ell(-q/2)),](/2012-wikipedia_en_all_nopic_01_2012/I/13dfdaa376cea3762bb04337b0517527.png) (which is understood to be 0 if q is odd)
(which is understood to be 0 if q is odd)
and abutting to
for −p − q > 1 + dim A.
K theory of the integers
Assuming the Quillen–Lichtenbaum conjecture and the Vandiver conjecture, the K-groups of the integers are given by Kn('Z) =
- 0 if n = 0 mod 8 and n > 0, Z if n = 0
- Z ⊕ Z/2 if n = 1 mod 8 and n > 1, Z/2 if n = 1.
- Z/ck ⊕ Z/2 if n = 2 mod 8
- Z/8dk if n = 3 mod 8
- 0 if n = 4 mod 8
- Z if n = 5 mod 8
- Z/ck if n = 6 mod 8
- Z/4dk if n = 7 mod 8
where ck/dk is the Bernoulli number B2k/k in lowest terms and n is 4k − 1 or 4k − 2 (Weibel 2005).
References
- Grayson, Daniel R. (1994), "Weight filtrations in algebraic K-theory", in Jannsen, Uwe; Kleiman, Steven; Serre, Jean-Pierre, Motives (Seattle, WA, 1991), Proc. Sympos. Pure Math., 55, Providence, R.I.: American Mathematical Society, pp. 207–237, ISBN 978-0-8218-1636-3, MR1265531, http://books.google.com/books?id=v2CuklFFV5IC&lpg=PA232
- Kahn, Bruno (1997), The Quillen-Lichtenbaum conjecture at the prime 2, http://www.math.uiuc.edu/K-theory/0208/QL2.pdf
- Lichtenbaum, Stephen (1973), "Values of zeta-functions, étale cohomology, and algebraic K-theory", in Bass, H., Algebraic K-theory, II: Classical algebraic K-theory and connections with arithmetic (Proc. Conf., Battelle Memorial Inst., Seattle, Wash., 1972), Lecture Notes in Mathematics, 342, Berlin, New York: Springer-Verlag, pp. 489–501, doi:10.1007/BFb0073737, ISBN 978-3-540-06435-0, MR0406981
- Quillen, Daniel (1975), "Higher algebraic K-theory", Proceedings of the International Congress of Mathematicians (Vancouver, B. C., 1974), Vol. 1, Canad. Math. Congress, Montreal, Que., pp. 171–176, MR0422392, http://mathunion.org/ICM/ICM1974.1/
- Rognes, J.; Weibel, Charles (2000), "Two-primary algebraic K-theory of rings of integers in number fields", Journal of the American Mathematical Society 13 (1): 1–54, doi:10.1090/S0894-0347-99-00317-3, ISSN 0894-0347, MR1697095, http://www.math.uiuc.edu/K-theory/0220
- Weibel, Charles (2005), "Algebraic K-theory of rings of integers in local and global fields", in Friedlander, Eric M.; Grayson, Daniel R., Handbook of K-theory. Vol. 1, Berlin, New York: Springer-Verlag, pp. 139–190, doi:10.1007/3-540-27855-9_5, ISBN 978-3-540-23019-9, MR2181823, http://www.math.uiuc.edu/K-theory/0691/